Daniel and Theo are trying to work out the height of a bird’s nest in their garden.
From Theo’s bedroom window, which is 4 m above the ground, the angle of depression of the nest is 10°. From Daniel’s position at the end of the garden, 8 m away from the house, the angle of elevation is 30°. Find the height (in meters) of the nest above the ground.

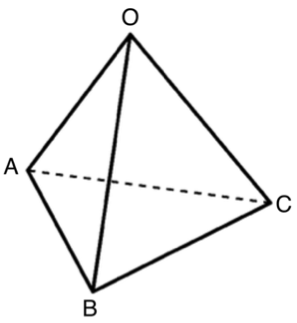
Pyramid $OABC$ is such that $OA=OB=OC=5$ cm and $AB=BC=CA=6$ cm.
Find the exact height (in cm) of the pyramid.

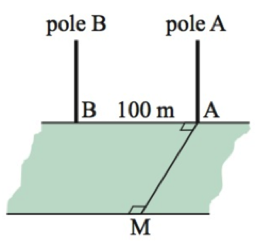
A man, M, positions himself on a river bank as in the diagram alongside, so he can observe two poles A and B of equal height on the opposite bank of the river. He finds the angle of elevation to the top of pole A is 22°, and the angle of elevation to the top of pole B is 19°. Determine the width of the river (in m), if he knows that A and B are 100 m apart.

A police helicopter departs from the police station, flying on a bearing of 330°. After flying for 1600 m, it receives a message to divert to a crime scene. It then changes direction to fly to the crime scene and its new path is on a bearing of 260°. The crime scene is 1800 m in a diagonal straight line from the police station. What bearing must the helicopter fly on to get back to the police station?

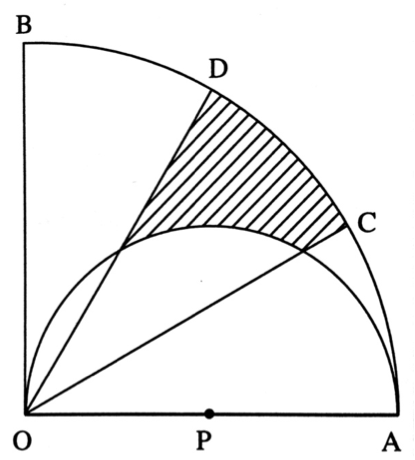
$AOB$ is a sector with radius $4$ and $\angle AOB=90°$. Point $P$ is the midpoint of $OA$ and a semicircle is drawn with center $P$. Points $C$ and $D$ lie on arc $AB$ such that lines $OC$ and $OC$ trisect $\angle AOB$ (trisect means to divide an angle into 3 equal parts). Find the exact are of the shaded region.