Chapter 29: Further Trigonometry
(29A) The unit circle
(29B) Area of a triangle using sine
(29C) The sine rule
(29D) The cosine rule
(29E) Problem solving with the sine and cosine rules
(29F) Trigonometry with compound shapes
(29G) Trigonometric graphs
(29H) Graphs of y=asin(bx) and y=acos(bx)
Extension Problems
A triangle’s perimeter and area have the same integer value.
What is the smallest possible area of the triangle?
Fill in the blanks with $sin$, $cos$ or $tan$ so that the multiplication of the rows and columns are correct.
*Each answer box corresponds to each row. Separate your answers using commas (for example: sin, tan, cos)
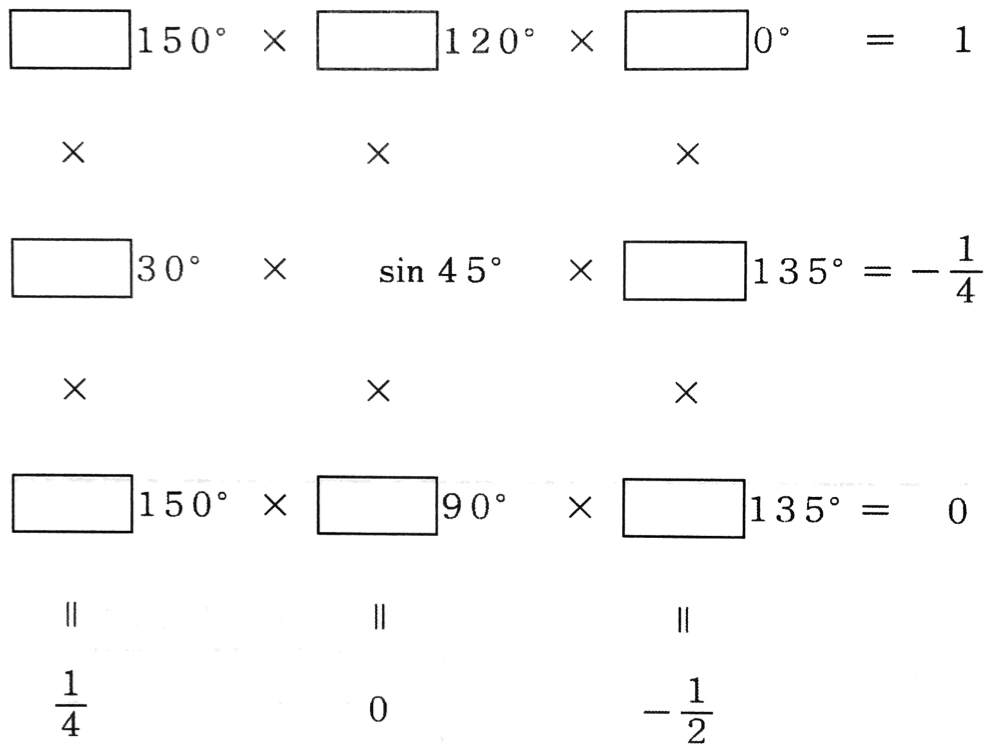
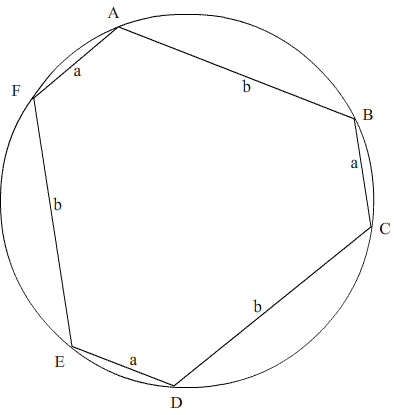
A hexagon is inscribed inside a circle.
The sides of the hexagon are alternately $a$ and $b$ units in length.
The sides of the hexagon are alternately $a$ and $b$ units in length.
Find the radius of the circle in terms of $a$ and $b$.
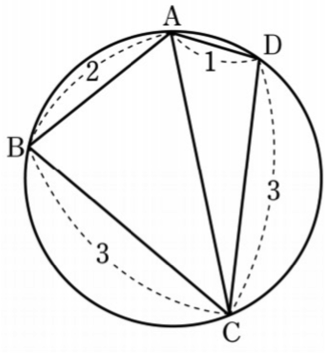
Find the exact length of diagonal $AC$ of the cyclic quadrilateral $ABCD$.
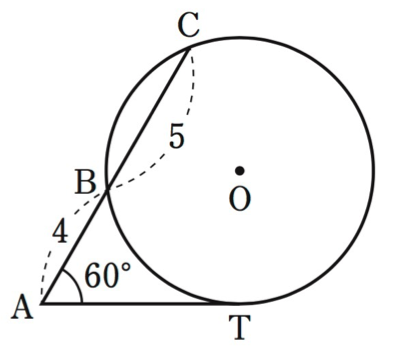
Line $AT$ is tangent to the circle at point $T$.
Find the exact radius of the circle shown.
Find the exact radius of the circle shown.
*Give your answer in the form $\frac{a\sqrt{b}}{c}$ where $a, b, c$ are integers.