Unit 10: Random Variables
Extension Problems
This is an extension of the Zelda Treasure Game you saw in class.
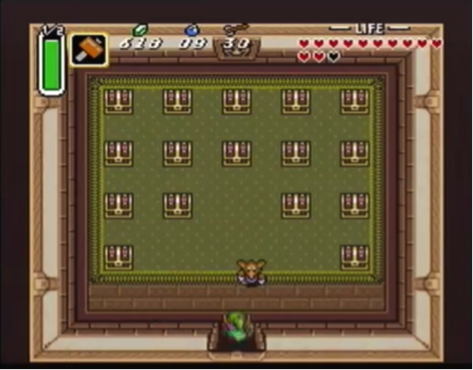
In this version, there are 16 treasure boxes. There are:
• twelve 1-rupee prizes
• three 50-rupee prizes
• one 100-rupee prizes
Find the expected value for this game.
*Give your answer as a decimal.
Three 6-sided fair dice are rolled and their sum is recorded. If the three dice show all different values, then stop. Otherwise, roll any dice with the same value again, and add the sum of these re-rolled dice to the previous sum. Continue this process until all three dice show different values, and let $X$ be the final total of the values of all the dice rolled.
Here is an example:
Roll 1: $5,5,3$ are thrown, for a running total of $13$.
Roll 2: The two dice showing $5$ are rolled again and come up $3,1$ for a running total of $13+4=17$. The three dice now show $3,1,3$.
Roll 3: The two dice showing $3$ are rolled again and come up $1,1$ for a running total of $17+2=19$. The three dice now show $1,1,1$.
Roll 4: All three dice are rolled again and come up $5,5,6$ for a running total of $19+16=35$.
Roll 5: The two dice showing $5$ are rolled again and come up $1,5$ for a running total of $35+6=41$. The three dice now show $1,5,6$ so we stop with $X=41$.
Find the expected value of $X$.
It can be written as a simplified fraction $\frac{a}{b}$, where $a$ and $b$ are positive integers.