Chapter 18: Similarity
(18A) Similarity
(18B) Similar triangles
(18C) Problem solving
(18D) Area and volume of similar shapes
Extension Problems
Solve for $x$.
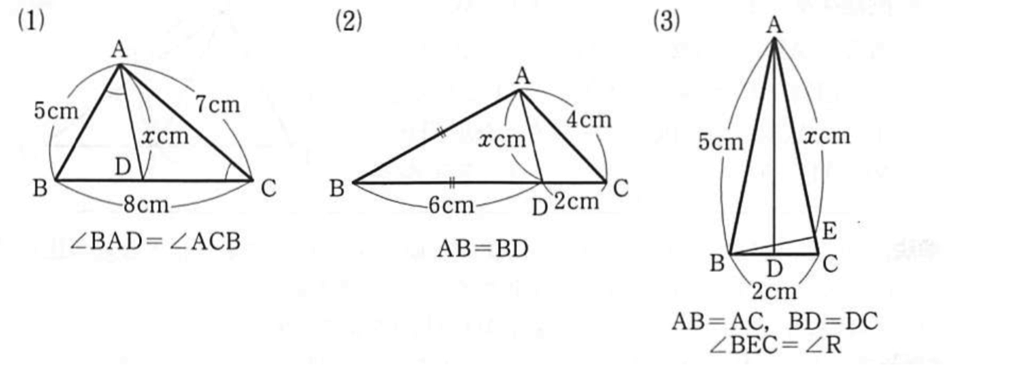
a)
b)
c)
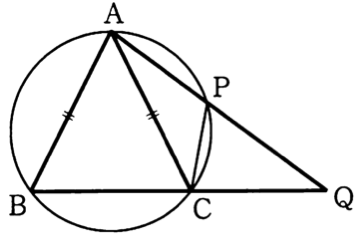
In the diagram, $AB=AC$, $P$ is on the circumference of the circle and $Q$ is the intersection of the extension of lines $AP$ and $BC$. If $AP=2$ and $AC=3$, find the length of $PQ$.
The diagram shows cyclic quadrilateral $ABCD$. $AB=AD$ and $P$ is the intersection of $AC$ and $BD$. If $BC=3,CD=6$ and $CP=2$, find the lengths of $AP$ and $BD$.
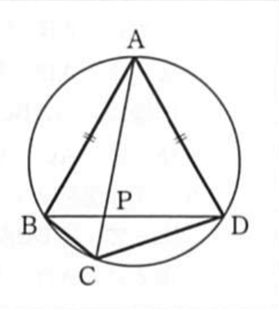
$AP$
$BD$
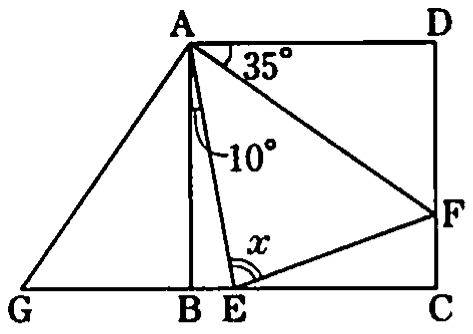
[Challenge] In the diagram, $ABCD$ is a square, point $G$ is on the extension of line $BC$ and $DF=BG$. Find $x$.
*You do not need to include the degree symbol
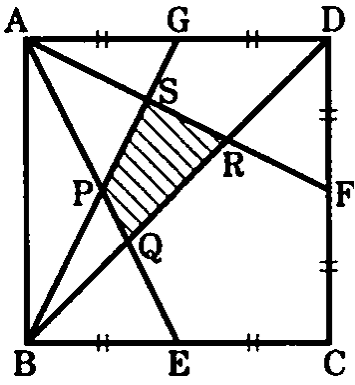
[Challenge] In the diagram shown, $ABCD$ is a square with sides of length $10$. $E,F$ and $G$ are all midpoints of the sides of the square. Calculate the area of quadrilateral $PQRS$.
*Give your answer as a fraction